Echantillonnage

L’altitude, l’humidité du sol ou la température à la surface du sol sont tous des phénomènes continus. Ce type de données doit être acquis par échantillonnage.

PHÉNOMÈNES CONTINUS

Les phénomènes continus (précipitation, altitude, humidité du sol, etc.) sont définis en tout point de l’espace et varient localement de manière graduelle et structurée.

PROPRIÉTÉS DE L’ÉCHANTILLONNAGE

L’échantillonnage est la démarche qui consiste à mesurer une variable d’intérêt en quelques points représentatifs d’une zone d’étude. L’interpolation est la méthode permettant de déduire la valeur en tout point de l’espace à partir des points d’échantillonnage. L’interpolation est applicable si l’estimation des valeurs prise par une variable en d’autres points de l’espace considéré possède une précision acceptable.

La première qualité d’un échantillonnage est celle d’être représentatif de tout l’espace considéré. Un échantillon est optimal s’il satisfait les conditions suivantes :

Les limites de la zone d’étude sont circonscrites selon des critères précis.

La répartition des échantillons est homogène et de densité optimale sur l’ensemble du territoire étudié.

Dans la pratique, les limites de la zone d’étude sont souvent fixées de manière progressive en s’appuyant sur les résultats précédents et la distribution des échantillons de départ est souvent arbitrairement choisie pour ensuite être complétée par de futurs échantillonnages dans des endroits jugés judicieux. Dans cette optique, l’utilisation de la notion de domaines est pertinente. Un domaine est une partie de la zone d’étude dans laquelle un phénomène est censé exister, présenter un comportement similaire et homogène. Le domaine est délimité lorsque ses limites sont connues et ouvert lorsque ses limites sont inconnues ou approximatives. Une même loi d’interpolation pourra donc être appliquée à l’ensemble d’un domaine ou à un sous-domaine lorsqu’une zone d’étude présente de l’hétérogénéité.

TYPES D’ÉCHANTILLONNAGE

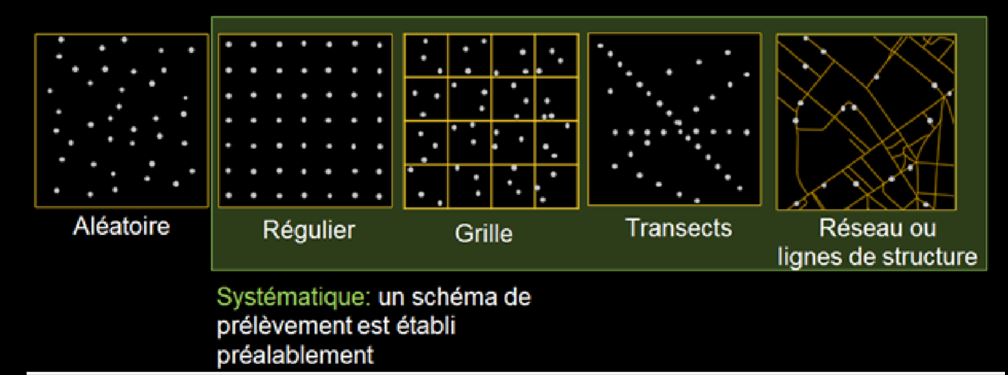
La quantité d’information préalable disponible sur le comportement d’un phénomène étudié influence fortement le choix du type d’échantillonnage. En absence d’information préalable, deux types d’échantillonnages peuvent être appliqués. L’échantillonnage aléatoire ou l’échantillonnage systématique (régulier, grille, transects ou lignes de structures). En présence d’information préalable, il est possible de mettre en place un échantillonnage le long de transects ou de lignes de structures (le long d’une rivière par exemple). Un échantillonnage exploratoire est mis en place afin de connaître progressivement le comportement d’un phénomène, lorsque celui-ci est invisible.

QUALITÉ DE L’ÉCHANTILLON

Un échantillon spatial est de qualité acceptable s’il représente géométriquement et thématiquement le comportement du phénomène étudié. L’obtention d’une densité optimale d’échantillonnage (densité de points permet de garantir une representation acceptable de la  distribution. L’échantillonnage d’une zone d’étude doit respecter certaines contraintes en vue de garantir une représentativité acceptable de la distribution et de garantir un processus de régionalisation par interpolation uniquement. Ces contraintes sont d’une part l’obtention d’une densité optimale de points d’échantillonnage et la constitution d’un ensemble de points d’échantillons extérieurs à la zone étudiée. Des échantillons extérieurs à la zone d’étude, pris dans une couronne suffisamment large, permettent d’éviter des effets de bords lors de l’interpolation. Thématiquement, les échantillons doivent représenter de la meilleure manière possible la dynamique des valeurs présente dans la région d’étude. On considère donc également la dimension temporelle afin que les valeurs thématiques soient correctement représentatives du comportement d’un phénomène pour une période de temps définie. Dans les cas où le phénomène présente une forte variabilité (température de l’air période de temps définie. Dans les cas où le phénomène présente une forte variabilité (température de l’air par exemple), il est possible de calculer un indice de tendance centrale pour exprimer le comportement général de la variable.

sources: EPFL Press, les BOOCs