Types de cartes thématiques

Une carte thématique est à la différence d’une carte générale ou carte topographique, une carte qui représente uniquement un type précis de donnée pour mieux qualifier les objets et les phénomènes disposés dans l’espace que par leur simple forme matérielle, en précisant leurs qualités. Ainsi, par exemple, les bois et les forêts ne seront plus de simples catégories du paysage, mais l’objet même de la représentation, pour en faire ressortir les caractéristiques, même matériellement peu ou pas visibles : types de boisements, propriétaires ou gestionnaires, modes d’exploitation.

Les cartes choroplèthes Les cartes en surfaces colorées

scientifiquement dénommées « cartes choroplèthes » permettent de représenter une variable numérique continue ou discrète, à l’exclusion des quantités ou des effectifs. Ce type de carte nécessite un maillage de la surface de la région étudiée en unités spatiales surfaciques représentées par des polygones. Afin de traduire, sur le plan géographique, les variations des données étudiées, chaque polygone est colorié. Dans ce but, différentes méthodes de discrétisation permettent le découpage en classes des variables continues afin d’affecter à chaque classe une couleur sélectionnée dans une gamme continue de couleurs chaudes, froides ou opposées. Une gamme « perroquet » traduit les valeurs des variables nominales. Il est fort utile de faire figurer en légende un histogramme qui présente l’étendue des classes vis-à vis de la distribution statistique. La carte de la population de race noire dans les districts sud-africains en 1991 ci-dessous recourt à une gamme de couleurs variant du bleu clair (faibles pourcentages de noirs) au marron (très fort pourcentages). Elle montre que, à l’échelle du pays considéré dans son ensemble, l’apartheid n’était pas seulement un système politique et social, mais aussi un fait géographique fondamental de l’organisation du territoire

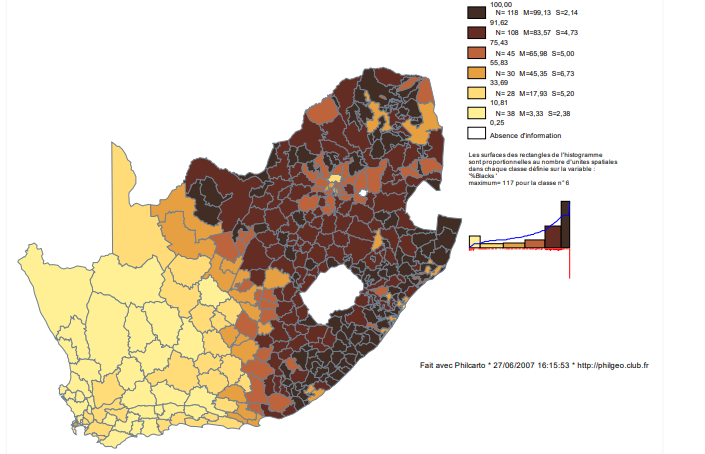
Les cartes en cercles proportionnels

sont destinées à représenter des quantités ou des effectifs. L’emploi de ce mode de représentation est plus délicat qu’il n’y paraît au premier abord : un calibrage des cercles s’avère nécessaire dans la plupart des cas, et plusieurs essais sont souvent indispensables pour obtenir un résultat satisfaisant. Une partie de la difficulté cartographique réside parfois dans la trop forte densité des unités spatiales provoquant des chevauchements qu’il faut gérer au mieux : les cercles les plus petits sont situés devant les cercles plus grands et un détourage (une circonférence tracée en blanc) permet de distinguer les petits cercles placés sur les grands. Ce mode de représentation n’est donc véritablement efficace que lorsque les unités spatiales ne sont pas en trop grand nombre (quelques centaines au maximum), et qu’elles sont réparties dans l’espace de manière relativement homogène.

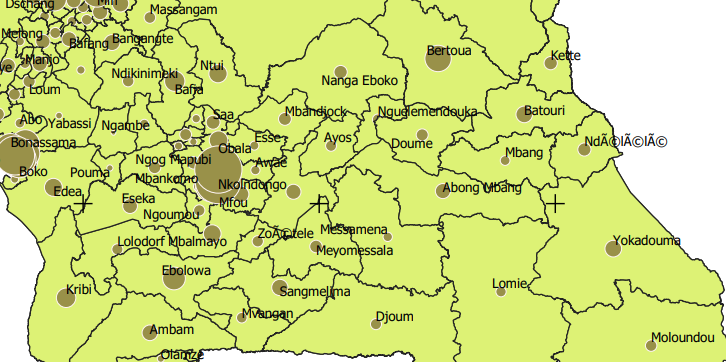
Les cartes en cercles proportionnels sur surfaces colorées

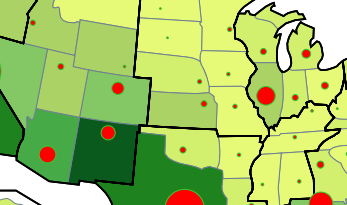
Comme les précédentes, les cartes en cercles proportionnels sur surfaces colorées permettent aussi de représenter simultanément des quantités ou des effectifs (cercles) et des valeurs numériques continues ou discrètes (couleurs des surfaces). Leur construction est encore plus sensible à la dimension des unités spatiales et à leur répartition dans l’espace. En effet, il faut éviter d’une part que les cercles se chevauchent, et d’autre part qu’ils recouvrent entièrement les surfaces colorées situées au-dessous d’eux (il est aussi possible de tracer seulement les circonférences de cercles, mais la lecture de la carte s’avère plus difficile). Dans la plupart des cas, une intervention du graphiste sur le placement des cercles est inévitable lors de la mise en page finale. La carte de la population « hispanique » aux États-Unis en 1996 (fig. 1.8) souligne l’importance de la Californie et du Texas, mais c’est au Nouveau-Mexique, sans doute pour des raisons historiques, que la proportion d’hispaniques est la plus élevée, toutefois avec un effectif beaucoup plus faible que les précédents. On observe d’autres implantations importantes, quoique secondaires, en Floride (immigration cubaine), et dans les régions industrielles de l’Illinois, de l’État de New[1]York et du New-Jersey.

Les cartes en demi-cercles affrontés

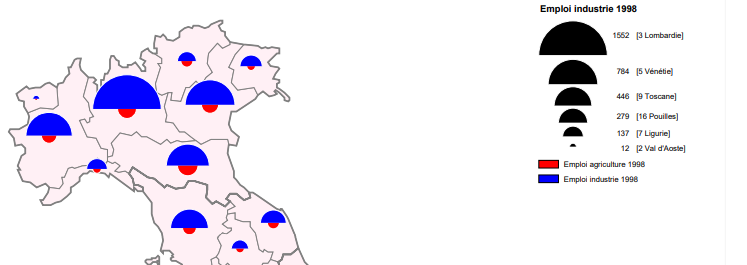
Une carte en demi-cercles affrontés représente simultanément deux variables portant sur des quantités ou des effectifs, à l’exclusion des pourcentages, taux, mesures ou catégories. Les cercles sont localisés sur un maillage ponctuel ; il s’agit de lieux de coordonnées X,Y, ou bien d’un point caractéristique de chaque polygone (centroïde, chef lieux…) d’un maillage surfacique. Un second maillage surfacique ou linéaire peut être superposé au maillage précédent pour former un habillage qui complète la carte et en facilite la lecture. Les cercles doivent être préalablement calibrés; cette opération consiste à choisir le diamètre du plus grand demi-cercle correspondant au maximum des deux variables : souvent, plusieurs essais sont nécessaires pour obtenir un résultat satisfaisant, c’est-à dire pour que le plus grand demi-cercle n’occupe pas une surface trop étendue, risquant en cela de masquer les autres demi-cercles, sans pour autant que le plus petit demi[1]cercle disparaisse. La légende comprend deux parties. En haut figure un échantillon de demi-cercles qui correspondent à des valeurs effectivement présentes sur la carte et relatives à la variable contenant le maximum, ceci afin de permettre au lecteur d’évaluer les quantités représentées en chaque point. Au-dessous, deux caissons colorés permettent d’identifier chacune des deux variables. Les inconvénients principaux de ce type de carte sont naturellement ceux des cartes en cercles proportionnels ; à ceux-ci s’ajoute l’obligation d’un diamètre assez grand pour permettre la perception des différences entre les demi-cercles affrontés, ce qui limite leur nombre de manière drastique. Ce type de carte ne doit donc pas être réalisé sur des fonds de cartes composés d’un grand nombre d’éléments cartographiques.

Les cartes en diagrammes à secteurs

Une carte en diagrammes à secteurs (figure désignée aussi par les noms « camembert » ou « pizza ») permet de représenter la composition d’une population en fonction de plusieurs catégories, chacune d’elles, enregistrée dans une variable, portant sur des quantités ou des effectifs, à l’exclusion des pourcentages, taux, mesures ou catégories. Le cercle représente la somme des effectifs des catégories de populations relatives à chaque élément cartographique ; pour que le résultat soit valide, il faut donc que ces effectifs puissent être sommés (ne pas additionner des kilos de carottes et de pommes de terre…). Les cercles sont localisés sur un maillage ponctuel ; il s’agit de lieux de coordonnées X,Y, ou bien d’un point caractéristique de chaque polygone (centroïde, chef lieux…) d’un maillage surfacique. Un second maillage surfacique ou linéaire peut être superposé au maillage précédent pour former un habillage qui complète la carte et en facilite la lecture. Les cercles doivent être préalablement calibrés ; cette opération consiste à choisir le diamètre du plus grand cercle : souvent, plusieurs essais sont nécessaires pour obtenir un résultat satisfaisant, c’est-à-dire pour que le plus grand cercle n’occupe pas une surface trop étendue, risquant en cela de masquer les autres cercles, sans pour autant que le plus petit cercle disparaisse. La légende comprend deux parties. En haut figure un échantillon de cercles qui correspondent à des valeurs effectivement présentes sur la carte et relatives à la somme des catégories de population, ceci afin de permettre au lecteur d’évaluer les quantités représentées en chaque point. Au-dessous, plusieurs caissons colorés permettent d’identifier chacun des secteurs. Les inconvénients principaux de ce type de carte sont naturellement ceux des cartes en cercles proportionnels ; à ceux-ci s’ajoute la quasi-impossibilité d’une lecture globale de la carte et de la recherche d’une organisation générale ; chaque diagramme doit être lu l’un après l’autre, ce qui limite leur nombre de manière drastique. Ce type de carte ne doit donc pas être réalisé sur des fonds de cartes composés d’un grand nombre d’éléments cartographiques.

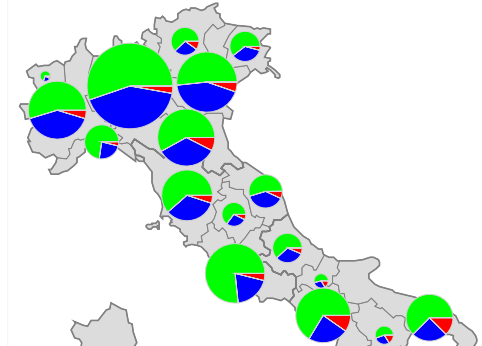
Les cartes en plages de niveaux et en bloc-diagramme

Les cartes en plages de niveaux reposent sur l’hypothèse que la variation des mesures statistiques présente une certaine continuité dans l’espace. C’est le cas, en météorologie pour les cartes de précipitations. En géographie humaine, une telle hypothèse est souvent trop forte, et la visualisation des données par des plages de niveaux n’est que la représentation des traits les plus saillants de la distribution. Les points de mesure forment un maillage ponctuel, régulier ou non ; il s’agit de lieux de coordonnées X,Y, ou bien d’un point caractéristique de chaque polygone (centroïde, chef lieux…) d’un maillage surfacique. Un second maillage surfacique ou linéaire peut être superposé au maillage précédent pour former un habillage qui complète la carte et en facilite la lecture. A partir du maillage ponctuel est dérivé un carroyage plus ou moins fin formant un maillage surfacique carré. Pour chaque centre de chaque carreau est estimée une valeur. Deux méthodes sont couramment employées pour ces estimations : la triangulation de Delaunay et le krigeage. Lorsque toutes les valeurs sont estimées pour chaque carreau, la cartographie en plages de niveaux devient un simple problème de carte choroplèthe, sachant que les limites des classes sont les limites des niveaux basés sur un espacement régulier, dans l’unité de mesure de la variable cartographiée. Le maillage coloré peut aussi faire l’objet d’une représentation par un bloc-diagramme, selon un angle de vue choisi par l’utilisateur. Les cartes de niveaux donnent de bons résultats si les valeurs ne sont pas spatialement indépendantes, caractéristique pouvant être évaluée par les coefficients d’autocorrélation spatiale de Moran et de Geary. La longueur des temps de calcul est l’inconvénient principal de ce type de carte.

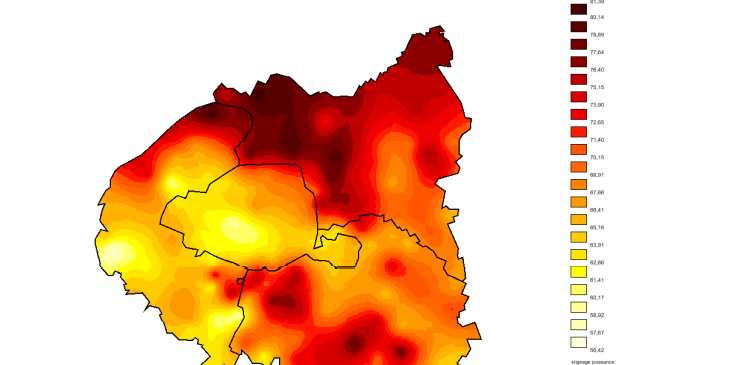
Les cartes en surfaces de tendances

Les cartes en surfaces de tendances reposent sur l’hypothèse que la variation des mesures statistiques présente une certaine continuité dans l’espace, hypothèse également à l’origine des cartes en plages de niveaux. La différence avec ces dernières réside dans la décomposition du phénomène supposé continu dans l’espace en composantes d’échelles se rapportant successivement à des espaces de plus en plus réduits. Aux valeurs calculées avec ces composantes s’ajoute un résidu local. Les points de mesure forment un maillage ponctuel, régulier ou non ; il s’agit de lieux de coordonnées X,Y, ou bien d’un point caractéristique de chaque polygone (centroïde, chef lieu…) d’un maillage surfacique. Un second maillage surfacique ou linéaire peut être superposé au maillage précédent pour former un habillage qui complète la carte et en facilite la lecture. A partir du maillage ponctuel est dérivé un carroyage plus ou moins fin formant un maillage surfacique carré. Pour chaque centre de chaque carreau sont estimées plusieurs valeurs à l’aide de fonctions polynomiales du type Z = f(X,Y)n où n est une puissance entière variant de 1 à 4 en pratique. Avec un polynôme de degré 4, on estime 4 valeurs pour chaque centre de chaque carreau. A ces fonctions est associé un taux de variance expliquée qui rend compte du plus ou moins bon ajustement des données par ces fonctions. Lorsque toutes les valeurs sont estimées pour chaque carreau, la cartographie en plages de niveaux devient un simple problème de carte choroplèthe, sachant que les limites des classes sont les limites des niveaux basés sur un espacement régulier, dans l’unité de mesure de la variable cartographiée. Le nombre de cartes de tendances est égal au plus grand degré du polynôme. Le maillage coloré peut aussi faire l’objet d’une représentation par un bloc-diagramme, selon un angle de vue choisi par l’utilisateur. Les cartes de tendances spatiales donnent de bons résultats si les valeurs ne sont effectivement pas spatialement indépendantes, caractéristique pouvant être évaluée par les coefficients d’autocorrélation spatiale de Moran et de Geary. La difficulté d’attribuer une signification géographique aux degrés successifs des polynômes constitue le principal inconvénient de cette technique. En pratique, on ne retient que les cartes absorbant un taux élevé de variance et présentant des configurations géographiques différentes. La carte des résidus permet ensuite d’évaluer l’importance de l’échelle locale dans la structuration spatiale du phénomène étudié.

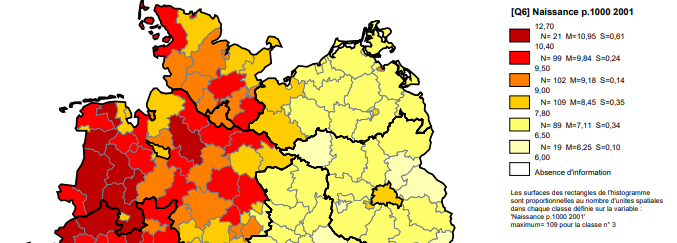
Les cartes en semis de points

Une carte en semis de points représente des quantités ou des effectifs par un nombre de points proportionnel à ces quantités ou à ces effectifs, à l’exclusion des pourcentages, taux, mesures ou catégories. Le maillage est surfacique ; les limites de ses éléments sont enregistrées sous forme de polygones. Un second maillage surfacique ou linéaire peut être superposé au premier pour former un habillage qui complète la carte et en facilite la lecture. A l’intérieur de chaque polygone sont placés au hasard des points en nombre proportionnel à l’effectif enregistré pour ce polygone. La valeur du point doit être préalablement calibrée, soit en choisissant de manière arbitraire cette valeur, soit en choisissant le nombre maximum de points qu’un polygone peut contenir ; dans ce cas, la valeur du point est égale au plus grand effectif à cartographier (le maximum de la variable) divisé par le nombre maximum des points choisi. Pour obtenir l’effet de densité souhaité, on peut aussi jouer sur la taille du point (de 1 à 5 pixels au plus), sur sa couleur (dans ce cas, tous les points de la carte ont la même couleur), et sur le fond sur lequel sont placés les points en maintenant ou non les contours des polygones, et en leur appliquant ou non une couleur. Tout l’art du cartographe consiste à choisir le résultat le plus conforme à la géographie du phénomène représenté. Mais le résultat dépend aussi du maillage surfacique qui doit être suffisamment détaillé pour que la géographie soit bien traduite, malgré l’abus lié au caractère aléatoire du placement des points sur la carte. Plusieurs tentatives sont souvent indispensables pour obtenir un résultat satisfaisant, mais le principal inconvénient de cette technique réside dans la nécessité de rappeler au lecteur que les points ne sont pas localisés au lieu précis d’enregistrement des quantités cartographiées. Des malentendus peuvent résulter de la mauvaise compréhension de la méthode par des non-cartographes. Un second inconvénient est lié au nombre total de points figurant sur la carte conduisant à des fichiers graphiques très lourds et donc difficiles à manipuler ensuite (corrections, habillage, impression).

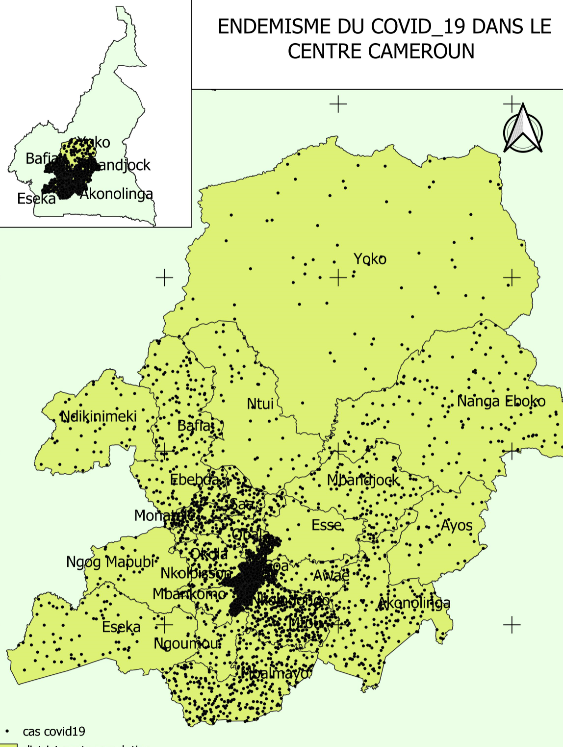
Les cartes de liens dites aussi en « oursins » Une carte de liens représente des relations entre des points de l’espace formant un maillage régulier ou non ; il s’agit de lieux de coordonnées X,Y, ou bien d’un point caractéristique de chaque polygone (centroïde, chef lieux…) d’un maillage surfacique. Un second maillage surfacique peut être superposé au maillage précédent pour former un habillage qui complète la carte et en facilite la lecture. Les relations sont figurées par des lignes droites qui joignent les points deux à deux. Ces lignes peuvent être coloriées en fonction des modalités d’une variable nominale. Ce mode de représentation est efficace lorsqu’on cherche à exprimer une organisation spatiale polarisée, car les liens s’arrangent alors à la manière des piquants d’un oursin. L’emploi de ce genre de carte présente de nombreuses limitations : risque d’enchevêtrement des liens en l’absence d’une forte organisation concentrique ; difficulté de lecture des couleurs des lignes.

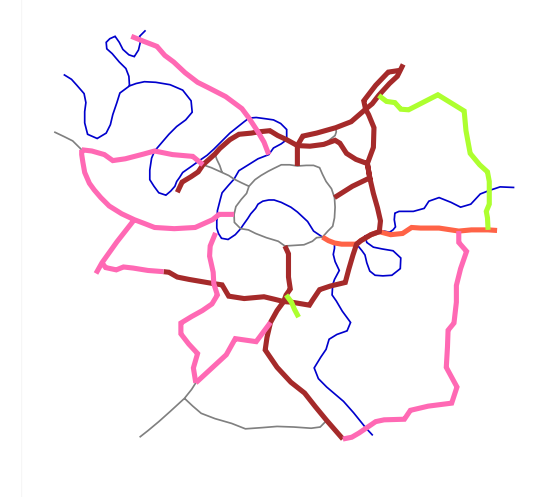
Les cartes de réseaux Les cartes de réseaux sont basées sur des lignes représentant les tronçons du réseau. La représentation des effectifs caractérisant chaque tronçon (flux s’écoulant dans le réseau ou autre mesure de quantité) fait appel à la variation des épaisseurs des lignes proportionnelle à ces effectifs. Pour figurer une modalité discrète issue d’une variable nominale, ou résultant d’un taux préalablement discrétisé, on fait appel à une gamme de couleur ordonnée (pour les taux) ou non (pour les modalités nominales). Il est possible de combiner variation d’épaisseur et variation de couleur pour représenter simultanément sur chaque tronçon un effectif et une modalité discrète. Ce mode de représentation est efficace si le maillage résultant du réseau n’est pas trop serré pour permettre la variation d’épaisseur qui, dans tous les cas, ne peut se faire que dans des limites relativement étroites : il apparaît difficile dans un format A4, et pour un réseau assez lâche, de tracer des lignes dont l’épaisseur dépasse un centimètre. Enfin, l’identification des couleurs des lignes par la légende suppose que ces couleurs soient appliquées sur des lignes assez épaisses, ce qui limite aussi le domaine d’application de ce genre de carte.

Les cartes de gravitation issues du modèle de Huff Les modèles de gravitation donnent une représentation simplifiée des aires d’attraction, c’est-à-dire du partage de l’espace environnant provoqué par l’accumulation des facteurs de centralité en un lieu, dans un espace isotrope. Par analogie avec la loi de gravitation universelle de Newton, les modèles élémentaires d’attraction urbaine reposent sur trois paramètres : la masse, la distance et l’exposant de la distance. La masse est un effectif mesuré en chaque lieu central ; il peut s’agir de la population active dans les services à haute valeur ajoutée (conseil financier, ingénierie des réseaux, etc.), du nombre de grands magasins, etc. La distance est mesurée à vol d’oiseau. Enfin, la valeur de l’exposant souligne que certains types d’interaction spatiale sont plus sensibles à la distance que d’autres, une valeur élevée traduisant une plus forte résistance au déplacement. Les points localisant les lieux centraux sont positionnés à l’aide de coordonnées X,Y formant un maillage ponctuel. Un second maillage surfacique ou linéaire peut être superposé au maillage précédent pour former un habillage qui complète la carte et en facilite la lecture. Les résultats de l’application du modèle de gravitation se traduisent par le tracé des lignes d’iso-attraction entre les centres pris deux à deux : à partir d’un centre donné, le franchissement de cette ligne signifie qu’un autre centre prend le relais et exerce sur l’espace environnant une attraction plus forte que le centre initial. La fermeture des lignes d’iso-attraction délimite les aires d’influence de chaque centre. Comme les lignes d’iso-attraction ne renseignent pas sur l’intensité des attractions, le modèle de Huff constitue un complément intéressant car il donne en chaque lieu une probabilité d’attraction à l’intérieur de chaque aire d’influence. Les probabilités d’attraction sont représentées par des cartes en plages de niveaux ou par des blocs-diagrammes. L’inconvénient fondamental des modèles de gravitation est l’isotropie de l’espace posée comme hypothèse ; le temps de calcul des ligne d’iso-attraction sont relativement long ; les fichiers graphiques des cartes en plages de niveaux sont volumineux.

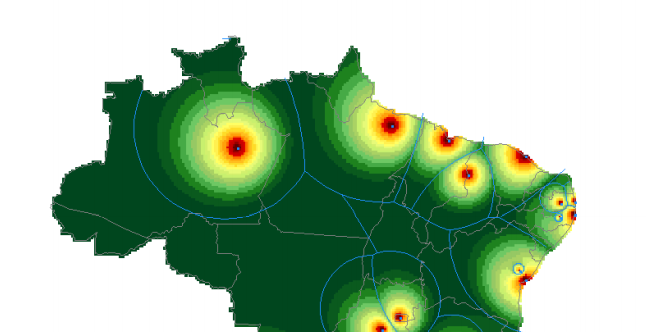
source: Phil Carto, Wikipédia